Stochastic Modeling – Definition, History, Applications

Stochastic modeling is the area of mathematics that deals with simulating and analyzing random processes and their outcomes. It involves the use of statistical methods to model and predict the behavior of uncertain variables.

The primary use of stochastic methods in finance is to use mathematical techniques to simulate and model the random motion of an asset price.

A Short History of Stochastic Modeling in Finance

The age of the field of financial mathematics which had been pioneered by Louis Bachelier, considered as the founding father of financial mathematics.

Louis Bachelier (1870 – 1946)

• Was the first to have applied mathematical models to the analysis of financial markets
• Stock prices evolve according to Brownian motion
• Used Brownian motion in his thesis “La théorie de la spéculation” to describe stock prices

Kiyoshi Itô (1940s)

• Developed stochastic calculus
• Itô integral with stochastic differential
• Itô’s lemma: differentiation of stochastic functions

Robert Merton (1969)

• Introduced stochastic calculus in finance to explain the price of financial products
• S ~ eW(t) >0 : The value of an underlying stays always positive!

Robert Merton, Fisher Black & Myron Scholes (1973)

• Published the famous work on option pricing
• The model allows to derive analytic expression for the fair price of call and put options
• A significant contribution to the growth of derivatives
• Merton and Scholes receive the Nobel price of economics in 1997 (F. Black had died in 1995)

Brownian Motion

A standard Brownian motion, or a Wiener process is a stochastic process (W(0), W(1), W(2)) with the following properties:

• It starts at the origin, W(0) = 0, and the sample paths are continuous
• The increments W(2)-W(1), W(3)-W(2),… are independent of each other
• The increments W(t)-W(s) are normally distributed N(0,√(t-s) )

Simply put, it is a random process that evolves continuously in time and its change over any time interval is a normal variate with mean zero and variance equalling the length of the time interval.

SEE ALSO: Derivatives 101: Overview & Types

The Black & Scholes Model

The simplest version of the model has the following asumptions:

• The stock price follows a geometric brownian motion with constant drift and volatility

dS = S ·μ · dt + S · σ· dW

S: value of underlying (stock, foreign exchange rate, etc)

µ : drift

σ : volatility (annualised)

t :  time (expressed in years)

W : Wiener process (Brownian)

Solution of The Black & Scholes Model

Call and Put options

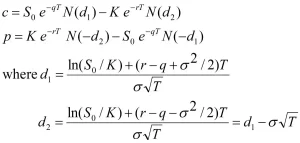
Interpretation of the Black & Scholes Formula

• N(d1): measures how far in the money the spot is expected to be if it finishes in the money
• N(d2): probability that spot finishes in the money

Call Price: Value of receiving the stock in the event of exercise minus cost of paying the strike price

The Black & Scholes formula depends on the spot, volatility, interest rates and time. None of these parameters involves the risk preference of the investor. Therefore, the Black & Scholes formula does not depend on any assumption about the risk preferences of the investors.

How Realistic Are The Assumptions of The Black & Scholes Model?

• In real markets the size of the fluctuations is not constant
• The underlying can make big jumps on some economic news
• Calculating the volatility is not trivial
• The process of the underlying is typically not lognormal
• Interest rates are not constant

Final Words

By using stochastic models, investors can better assess their investment strategies, and optimize asset allocation.

At the core of stochastic modeling is stochastic process, which is a collection of random variables, representing the evolution of some system of random values.