Option Greeks: How to Use Them to Measure Risk

Understanding the risk types that an option might involve is crucial for all market participants. The idea behind Greeks is to measure the different types of risks; they represent the sensitivity of the option to different factors.

KEY TAKEAWAYS

• The main Greeks are delta (sensitivity to the underlying price), gamma (sensitivity of delta to the underlying price), theta (sensitivity to time), rho (sensitivity to the risk-free rate), and vega (sensitivity to the volatility).
• They represent sensitivities of the portfolio with respect to market parameters.
• They allow us to monitor the risk of the portfolio.
• They can be applied to a single derivative or to a portfolio of derivatives.

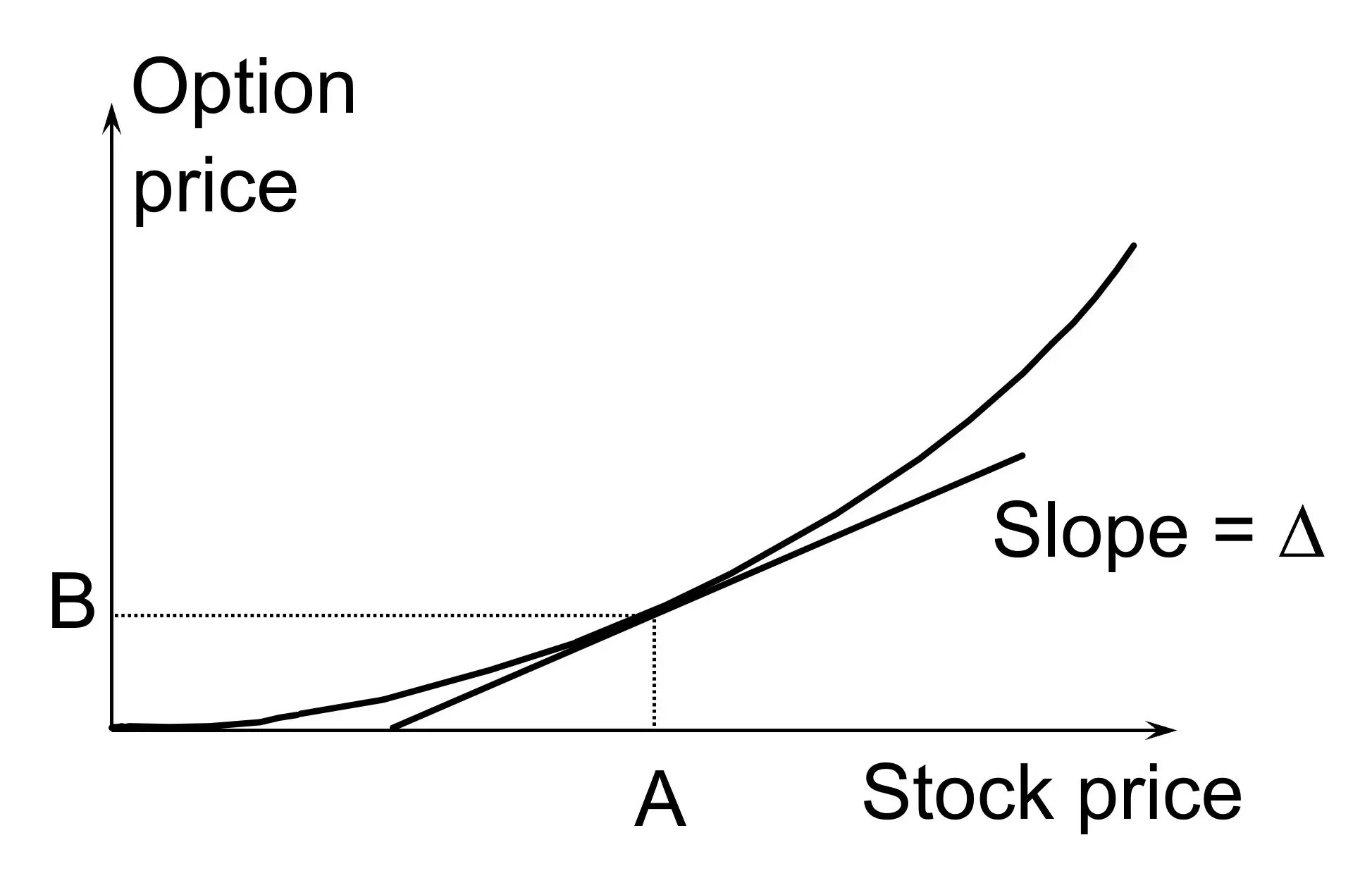
1. Delta

Delta is the rate of change of the option price with respect to the underlying. The delta of a call option has a range between 0 and 1, while the delta of a put option has a range between 0 and -1.

The delta of an option is its sensitivity to the price of the underlying asset.

Related: Options Contract: Overview & Types

When interest rates change, an option’s delta will change in the same direction. Call values are more sensitive and put values are less sensitive to changes in price of the underlying asset at higher interest rates, and vice versa.

2. Gamma

Gamma is the more interesting parameter and it measures the sensitivity of an option’s delta to changes in the price of the underlying asset. Gamma is the second derivative of the derivative value with respect to the underlying price.

If the option is around being at-the-money, its gamma is greatest. This means that the position’s price exposure is likely to change a lot when the stock price moves around the level of the strike price. For deep in- or out-of-the money options, gamma is close to zero and delta does not change much with
the stock price.

3. Theta

Theta of a derivative (or portfolio of derivatives) is the rate of change of the value with respect to the passage of time. The theta of a call or put  is usually negative. This means that, if time passes with the price of the underlying asset and its volatility remaining the same, the value of a long option declines.

4. Rho

Rho is the rate of change of the value of a derivative with respect to the interest rate. This measures sensitivity to the interest rate.

Holding the other parameters constant, as interest rates increase, call prices will increase and put prices will decrease. Intuitively, a higher rate of interest means a lower present value of the exercise price, implying a higher intrinsic value for the call and a lower value for the put.

5. Vega

Vega is the rate of change of the value of a derivatives portfolio with respect to volatility. It represents the change in value of a derivative with if market volatility moves by 1%.

The Bottom Line

It is often useful to analyze how a given Greek changes if some market parameters change. Such analysis might help us to understand risks better.

Traders usually ensure that their portfolios are delta-neutral at least once a day. Whenever the opportunity arises, they improve gamma and vega. As portfolio becomes larger hedging becomes less expensive.

YOU MAY ALSO LIKE: 

• Derivatives 101: Overview & Types
• Swaps: Definition & Types
• Understanding Portfolio Theory: Overview & Formulas