Black-Scholes Model: Definition, Formula, Examples and Uses
The Black-Scholes Model is one of the most powerful tools in finance, especially in options trading. Whether you’re a professional trader or just starting out, you need to understand this model to value options and make informed trading decisions.
In this article, we’ll go into the definition, formula and practical uses of the Black-Scholes Model with examples to help you get a better understanding of it.
What is the Black-Scholes Model?
The Black-Scholes Model is a mathematical model to calculate the theoretical price of European style options. It was developed by economists Fischer Black and Myron Scholes, along with Robert Merton in the early 1970s. Scholes and Merton were awarded the 1997 Nobel Prize in Economics for this.
The Black-Scholes Model is used to calculate the fair value of an option which gives the holder the right but not the obligation to buy or sell an underlying asset at a predetermined price before or on a specific expiration date.
If you’re interested in derivatives markets, check out our articles on “Financial Derivatives: Definitions and Types“, “Derivatives 101: Overview & Types“, and “Forward Contracts vs. Futures Contracts: Key Points & Differences“.
Black-Scholes Formula
The Black-Scholes formula calculates the price of a European call or put option using:
- S: Current price of the underlying asset
- K: Strike price of the option
- T: Time to expiration (in years)
- r: Risk-free interest rate (continuously compounded)
- σ (sigma): Volatility of the underlying asset
- N(x): Cumulative distribution function of the standard normal distribution
Call option:
C =S × N(d1) − K × e^−rT × N(d2)
Put option:
P = K × e^−rT × N(−d2) − S × N(−d1)
Where:
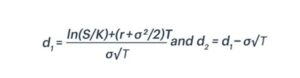
Breaking it Down
To really get a better understanding of how the Black-Scholes Model works, let’s break it down step by step.
- S × N(d1): This is the present value of the expected payoff from buying the underlying asset at the current price.
- K × e^−rT × N(d2): This is the present value of the expected payoff from exercising the option at the strike price.
- N(d1) and N(d2): These are probabilities from the standard normal distribution which estimate the probability of the option being exercised profitably.
Essentially, the Black-Scholes Model is the difference between the current price and the strike price adjusted for the probability of those prices being reached by the option’s expiration.
Example: Call Option Price
Let’s see how the Black-Scholes Model is used in practice. Assume you want to calculate the price of a European call option with the following details:
- Current stock price (S): $100
- Strike price (K): $95
- Time to expiration (T): 1 year
- Risk-free interest rate (r): 5%
- Volatility (σ): 20%
When we put the given figures in the formula, we find d1 = 0.60, and d2 = 0.40. And using a standard normal distribution table, we find N(0.60) = 0.7257, N(0.40) = 0.6554
Finally, we can calculate the call option price as:
C = 100 × 0.7257 − 95 × e^−(0.05×1) × 0.6554
C = 12.66
So, the call option is worth $12.66.
Example: Put Option Price
Assume you want to calculate the price of a European put option with the following details:
- Current stock price (S): $100
- Strike price (K): $105
- Time to expiration (T): 1 year
- Risk-free interest rate (r): 5%
- Volatility (σ): 20%
When we put the given figures in the formula, we find d1 = 0.106, and d2 = −0.094. And using a standard normal distribution table, we find N(0.106) = 0.5426, N(−0.094) = 0.4620
So, we can calculate the put option price as:
P = 105 × e^(−0.05×1) × N(0.094) − 100 × N(−0.106)
P = 7.78 (which means the put option is worth $7.78
Practical Uses of the Black-Scholes Model
The Black-Scholes Model isn’t just a theory; it has real uses for traders, investors and financial institutions. Here are some of them:
- Options Pricing: The most common use of the Black-Scholes Model is to price European options. By plugging in the numbers, you can see if an option is fairly priced, overpriced or underpriced and make better trading decisions.
- Hedging Strategies: The model helps in creating hedging strategies by calculating the “Greeks” which are the different sensitivities of the option’s price. For example, delta (Δ) is the change in the option’s price for a change in the underlying asset’s price. This is critical in creating risk neutral portfolios. SEE MORE: Option Greeks: How to Use Them to Measure Risk
- Risk Management: Financial institutions use the Black-Scholes Model to measure the risk of their options positions. By understanding the factors that affect option pricing, they can better manage losses.
- Derivatives Valuation: Beyond options, the Black-Scholes Model is the foundation for pricing other derivatives. Its influence extends to financial engineering where complex financial instruments are modelled and valued. SEE ALSO: What is Financial Engineering?
The Bottom Line
The Black-Scholes Model is changed the way we price options. It gives us a clear and systematic way to value European options, so we can make informed decisions in the options trading.
It has its limitations but it’s a cornerstone of modern finance and has applications way beyond just options pricing. Whether you’re trading, hedging or risk management, you need to understand the Black-Scholes Model if you’re in the financial markets.
More Resources
Thank you for reading our guide to Black-Scholes Model. To keep learning and developing your knowledge of financial derivatives, we highly recommend the additional resources below:
